This is when you are using visuals, pictures, and manipulatives to enhance your understanding for math.
Why is visual mathematics important?
Our brain is made up of different pathways that connect to each other to help us understand mathematical concepts. The more areas of our brain that we can use at one time to understand a new concept, the stronger the pathways will become.
Fast mathematics is not always the most important idea, strong math students make deep connections and are able to visualize ideas to be able to recreate them later.
Think New Thoughts
Below are some TedTalks from YouTube that will help you evoke new thoughts about math. I encourage you to watch these at home to broaden your mindset about math.
"Did you know that if you insert a statistic into a sentence that 92% of people are more likely to believe you?" -- Did you fall for that? Then click here to hear more!
A person who is dyslexic talks about teaching without words and how we can still be successful in math. All students can benefit profoundly without any written words at all.
Jo Boaler talks about being "born with a math brain."
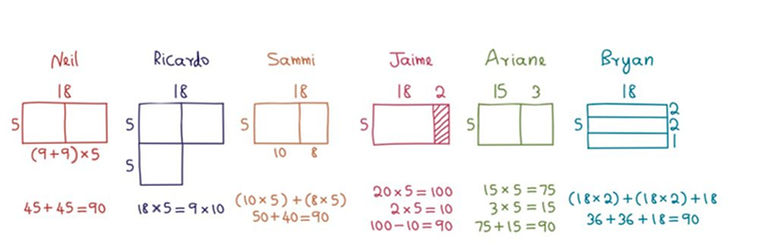
Examples of Visual Mathematics
Do you know the trick with the 9's on multiplying? Now you can multiply any numbers that are 6-10 on your fingers too! Use this to check your knowledge whenever you are doubting your mental math.
This is a simple and productive way to visualize mathematics. Showing your work in class will help you visually see what your next step would be. Writing out your steps will help you replicate those steps when problems get harder. If you get stuck, draw a picture or stop and ask yourself if what your doing makes sense in the context of the problem.
Nets are a way to "unfold" a three dimensional object into simple one dimensional shapes. These are helpful with understanding area formulas. A cube is made up of six squares, so if you know the that the area of one square is just “side squared” or “base times height” then the formula for a three dimensional cube with six squares would be “6 times side squared”. We can also understand the area of a triangle just by knowing the area of a square once again. A square folded diagonally is just 2 triangles, so if the area of a square is “base times height” and half of a square is a triangle, then the area of a triangle is “1/2 times base times height."
Foldables
This is Mrs. Emschweiler's favorite way to help understand a topic. Start with a blank sheet of paper, fold it to make sections, think about how you can break a topic into different pieces and write about it in each section. If you are using it to summarize a big topic, then each section could be about a different key ideas in the big idea. If you are using it to summarize one key idea, then one way you could use your foldable is to use sections for examples, non-examples, definitions in your own words, or pictures to summarize the topic. Another way you could use your foldable is to designate each section for different ways to solve the same problem. If you run out of ways to solve the problem differently and have a leftover section, use that section to write about which way you think is best and why.
Here are some examples of foldables we will make this year in Chapter 9.
Walk the Graph
This year we will be doing a lot of graphing. Any time a student is stuck with graphing and plotting points, it might be helpful to "walk it out" by using tape on the floor as an x and y axis.
Here is also a fun game with walking a graph.
Click here to see more activities with visual mathematics that even use Uber and Lyft.

